Author: DLorimer

BAD! Or, at least, that’s the general view. As always, however, there isn’t a simple answer.

I once made a casual statement that volatility on a renewable energy yield assessment for a debt transaction I was working on was beneficial from a creditworthiness perspective. My client at the time (the lender) was adamantly opposed to the statement. Since it’s generally the case that greater volatility is bad for a transaction, (and the client is always correct!), let’s look at why it’s bad.

Project finance is, inter alia, lending a principal sum against a set of predictable cash flows. Greater volatility of yield implies less predictability and therefore greater risk of being unable to meet payments when they fall due. This means higher probability of default, higher pricing, less debt-bearing capacity and so on. So volatility is generally bad for a transaction, and perhaps especially so for equity, since debt will only ever lend up to a level of risk which it is comfortable with (one assumes!).

On the other hand, there’s the concept of Upside Risk (https://en.wikipedia.org/wiki/Upside_risk). This is the possibility of a gain in the value of an investment. All other things being equal, the greater the (statistical) downside risk in an investment, the greater the (statistical) upside risk. Upside risk is also applicable to a yield assessment, since it is, after all, a statistical assessment.

Moreover, lenders will usually lend up to a maximum amount limited by the P90 yield assessment. (and the debt:equity ratio, debt service cover ratio levels and other metrics imposed by their credit committees). Assuming the yield assessment is reasonable in determining the P50 yield and the standard deviation of the yield, and that a Normal distribution is a reasonable approximation of the actual random distribution of the yield, it’s helpful to examine the downside and upside scenarios in terms of conditional probabilities (https://en.wikipedia.org/wiki/Conditional_probability, for those of you who like numbers!):

• Downside scenario: All other things being equal, the expected yield given the actual yield is less than the P90 level will be lower for a plant with a higher-volatility energy yield than for the same plant with a lower-volatility energy yield.

Obviously when considering such a scenario, lenders would like a lower volatility energy yield assessment, so as to limit possible downside scenarios to a smaller loss (or failure to repay).

 

• Upside scenario: All other things being equal, the expected yield given the actual yield is greater than the P90 level will be higher for a plant with a higher-volatility energy yield than for the same plant with a lower-volatility energy yield.

 

In this scenario, higher-volatility implies greater CFADS.

Consequently, it is reasonable to balance the risks and benefits of the two scenarios. Under the downside scenario, the risk is that the yield may be insufficient to ensure debt service, particularly if the cover ratios under the P90 base case were tight to begin with. It is worth noting that (assuming the correctness of the yield assessment) this risk has less than a 10% probability of arising (because we’re using a P90, the base case cover ratios being > 1.0x and because Normal distributions with the standard deviations typical of renewable energy projects are relatively long-tailed).

The upside scenario, on the other hand, encompasses 90% of predicted years’ energy outcomes, assuming we’re using a 1-year P90. This in turn means that the CFADS will be larger than under the P90 base case in most years, and, simply, cash can be used to mitigate many risks. The nature of those risks is, of course, very much dependent on how well they are mitigated through the contractual protections built into the project documents. If all risks other than yield are 100% contracted away to the project’s reliable and creditworthy counterparties, then the protection offered by additional cash is worth less than if only a portion of that risk is dealt with. Similarly, if DSCRs are very healthy using the P90 cash flows, the marginal benefit of yet more cash is smaller.

The question then becomes one of whether the benefit of additional cash in (probably) nine out of ten years to mitigate risks which may arise in those years, is greater than the risk of a greater expected underperformance in the one (probably!) year in ten when yield is lower than the P90 level. This is a slightly more difficult evaluation than an all-encompassing perspective that volatility is bad. However, it also offers benefits which may be proposed to a credit committee, for those transactors with a higher-volatility project!

The energy yield assessment is a fundamental requirement for any new wind or solar project, with both developers and lenders spending considerable time with their respective advisers to understand the underlying wind or solar regime. The remainder of this article speaks predominantly to wind energy yield assessment, but the same principles can be applied to solar projects.

Before we start, a short discussion around P50 and P90: The P50 energy yield estimate is the estimate of the energy yield which the energy yield modeller estimates will be exceeded with a 50% probability. Similarly, the P90 energy yield estimate is the estimate of the energy yield which the energy yield modeller estimates will be exceeded with a 90% probability. Consequently, the P90 estimate is lower than the P50 estimate. Although P-levels are usually quoted as annualised figures, the application periods can differ: Hence you may see reference to a 1-year P90 or a 10-year P90. This is simply the estimate of the amount of energy which the modeller estimates will be exceeded in a 1-year period or a 10-year period (multiplied by 10, since it is an annualised figure). They differ because the P90 is a function of the median energy yield estimate and the standard deviation of the energy yield estimate. In the case of the 10-year P90, the uncertainty associated with the estimate is spread over 10 years, so that a bad year can be offset by a good year within the period; or statistically speaking, a larger sample size reduces the variance associated with the estimate. As an aside, because the P50 is simply the median of the probability distribution and takes no account of variance, there would be no difference between the 1-year and 10-year P50 estimates. A P90 estimate is typically used for the banker’s base case model, and a P50 for the equity case. Project financiers should consider whether the P90 estimate is a 1-year of 10-year figure in determining their cover ratios – particularly if the numbers are tight.

The process of estimating the energy yield for a wind farm involves the following steps:

1. Implementation of an on-site wind data measurement campaign
2. Estimation of the average long-term wind speed at the site
3. Estimation of the energy yield (which is driven by the characteristics of the particular wind turbine selected for a wind farm)
4. Uncertainty analysis (further consideration of the uncertainties associated with the particular yield estimation, e.g. short data record representing a long-term wind regime, accuracy of measurement equipment, etc.)

Given the significant number of wind projects implemented over the last 30 years globally, the process of estimating the energy yield for a wind farm is nowadays well understood, with established internationally accepted norms and standards. The above four steps are described in more detail below.

 

Measurement Campaign

Wind projects require on-site measurement campaigns in order generate an energy yield for a potential wind farm. Data is collected using a wind mast and anemometers. Ideally the mast should be at turbine hub height to eliminate uncertainty associated with wind shear (vertical movement of air) and uncertainty associated with different wind speeds at different heights.

Typically one or more wind masts are placed within circa two kilometres of the furthest proposed turbine locations in the future wind farm. Each mast will have a number of cup anemometers (a device for measuring wind speed) at intervals up the mast up to the hub height of the proposed turbines, as well as wind vanes for measuring wind direction, thermometers and possibly barometers for measuring air pressure.

The period over which data should be collected should be greater than one year in order to assess the effects of seasonality on the wind resource. Any additional period in excess of one year is beneficial in that it further reduces the standard deviation of the data sample and allows some or better identification of long-term trends. For this reason, nearby meteorological station data is often correlated with the data derived from the on-site mast and, should the correlation be sufficiently high, used to establish whether wind speeds experienced in the 12-month measurement period are above or below the long-term average.

The topography of the site, and in particular the extent of rough terrain and surfaces such as mountainous terrain, trees, tall buildings and other wind turbines effect the flow of air across the site. In a relatively low-complexity (smooth, few trees or other such features) site, industry experts recommend that measurement masts are placed within one to two kilometers of the turbines.

Data is collected at short intervals, such as every 10 minutes. Before further analysis, the data is usually checked and cleaned for any anomalies (e.g. periods where equipment has failed).

 

Estimation of Long-Term Wind Speed

The collected data is used to fit a Weibull probability distribution function, which represents the statistical distribution of the wind speed. A normal distribution is sometimes used as a tractable approximation to the Weibull function.

If there is a nearby meteorological station with wind measurement data which is sufficiently highly correlated with the on-site data, its data may be used to determine long-term trends in the on-site wind data. For example, it may be possible to determine whether the measured year is abnormally windy or still. If such long-term information is not available (which is the case in most instances), then this is addressed in the uncertainty analysis (see below), i.e. the standard deviation of the energy yield estimate is increased, resulting in a lower P90 estimate.

Once the long-term average wind speed for a mast location has been derived, the wind speed is in turn estimated for each future turbine location, which will then enable an estimation of the overall energy yield for the wind farm, discussed further below.

 

Energy Yield Estimation

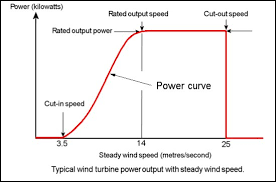
For each turbine location, the wind distribution is transformed using either a theoretical or empirical power curve associated with the proposed wind turbine, thereby converting the wind speed distribution into an energy output distribution. The power curve is provided by the turbine manufacturer, and it is noteworthy that the turbine manufacturer will typically provide a power output guarantee supported by performance damages, with the result that the power curves are unlikely to be unduly optimistic. An example of a power curve is displayed below:

(Source: www.wind-power-program.com)

In addition to fitting the probability distribution function for wind speed, the data is used to determine the extent of turbulence (very short duration gusting), changes in wind direction and wind shear (vertical air movement), all of which are incorporated into the yield estimation model for the power output.

While a measurement mast as described may accurately determine the output of a wind turbine on the same spot, wind speeds and other relevant meteorological conditions will change as turbines are sited further away from the measurement location. Consequently, the wind yield modeller will typically build a computational fluid dynamics model which takes account of the topography of the proposed site, including the wake effect of the turbines upon each other. The layout of the wind farm, or micro-siting, is determined by means of optimising the positioning of the turbines with respect to energy yield.

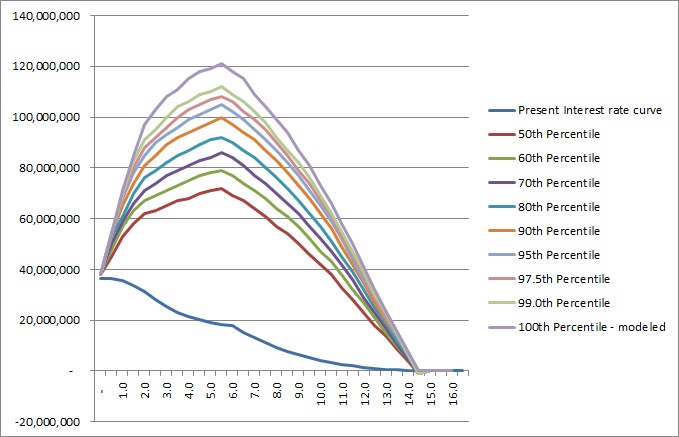
The energy yield modeller deals with additional influences upon the plant and uncertainty in the modelling variables by modifying the expected energy yield. An example of this taken from a wind energy  yield report is shown below:

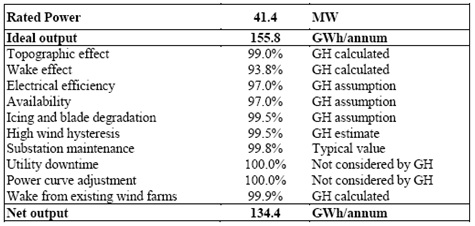
In this example, the modeller has decreased the expected energy yield, which is the central estimate, or the P50 energy yield. Going back to our discussion about probability distributions, the figure of 134.4 GWh/year is the modeller’s best estimate of the yield, and is therefore the median in the probability distribution.

To obtain the energy yield with a higher certainty (e.g. the P90 yield, or the yield that can be expected to be exceeded 90% of time) an uncertainty analysis is required which is discussed further below. Naturally, the P90 yield will be lower than the P50 yield. Regarding the losses calculated above, these particular loss factors attributed to the plant result in a certain loss (of 21.4GWh/annum in our example) but no change in volatility, and consequently reduce the P50 yield estimate and the P90 yield estimate by the same amount.

 

Uncertainty Analysis

There are a number of sources of uncertainty which feed into the standard deviation of the wind probability distribution function, thereby into the standard deviation of the energy yield probability distribution function, and which therefore decrease the P90 yield estimate, but not the P50 yield estimate. These sources of uncertainty are broadly split into two types, being:

• The underlying “true” volatility of the wind resource (it could actually blow more this year than next or vice versa); and
• The uncertainty associated with the calculations made along the way. Included here is the uncertainty introduced by using a short data record (e.g. 12 months’ on site data) , accuracy of the measurement equipment, etc.

Using this final power output probability distribution function, the energy modeller is able to determine confidence limits for the energy output of the plant. In particular:

• A P50 estimate is the median yield which is typically used for determining the equity case, and
• A P90 case, being the power output likely to be exceeded with a probability of 90%, is typically used as the power output assumption in the lenders’ base case.

Various P-values are used for debt structuring purposes, with the EU market commonly using a 10-year P90 yield, as alluded to above. The type of financing structure may also determine which P-value is used, e.g. higher gearing (80%+ debt) may need to be structured using a more conservative P-value. In South Africa, some projects have been structured using 1-year, and others 10-year P90 values. Ultimately, each project should be reviewed independently, by reviewing the underlying energy yield assessment (unique for each site) and conducting sensitivity analyses to assess how uncertainty in the energy yield impacts the expected financial performance of a project.

A little more on regional standards: The EU commonly uses a 10-year P90 with a minimum 1.30x DSCR, while the US market commonly uses a P99 with a minimum 1.0x DSCR. Please don’t take these as gospel, though. Rather assess your project and determine the suitability of any given regime (or use more than one!)

Comparing wind with solar projects, the variability in a wind energy resource assessment is typically higher than that in PV, and significantly higher than for CSP (concentrated solar thermal power). For example, the P50 yield typically exceeds the 1-year P90 yield in wind transactions by between 15% and 25% of the P90 yield. A Moody’s research paper for 34 wind farms in the USA provided an average P50/1-year P90 exceedence of 17.6%. This compares to a commensurate difference in PV of circa 8% – 10% (also using 1-year P90).

Breaking it down further, the size of the standard deviation of the energy yield estimate is a function of:

1)  The estimated volatility of the wind regime; and

2) The uncertainty relating the model of the plant. I.e. How that wind regime translates into energy output.

The impact of the volatility of the wind regime can have a significantly different impact for different locations and different turbine choices.  Consider the turbine power output curve:

In particular, for a given volatility of wind speed, a wind regime in which the median wind speed is close to the wind speed required to top out the power curve (14 m/s in the illustrated graph) will have a much power output volatility  than that of a wind regime where the median wind speed is in the middle of the curve (circa 9 m/s). This is simply a function of the relative steepness of the curve at each of these two points – the steeper the curve, the greater the change in energy yield per m/s change in wind speed.

Consequently, although it is obvious that faster average wind speeds are better for a wind farm, there’s also a beneficial second-order effect in that they will probably also reduce the volatility of the energy yield.

It is important to keep in mind that the difference between the P90 and the P50 (for our discussion defined as “yield volatility”, which is not a formal industry term) does not influence the probability that the lenders’ base case will be achieved or exceeded – being, of course, 90%, assuming the competence of the modeller.

 

Different counterparties to the project may be required to provide guarantees that their performance will meet a certain minimum standard. For example, the Engineering, Procurement and Construction contractor may be required to guarantee the date of completion, and the minimum performance levels of the plant. Similarly, the operator may be required to guarantee a certain minimum availability for the plant, or the fuel supplier the calorific value of the fuel.

In assessing guarantees , whether as project or lender, it’s helpful to examine three specific characteristics of the guarantees, being effectiveness, importance and reliance:

Effectiveness:

Is the guarantee effective in covering lost revenues? To do this, compare the rate of accrual of the guarantees per day of delay or per percentage point downside performance with the resulting loss of revenues.

For example, if the delay liquidated damages (LDs) accrue at a rate of USD 0.5m / day, and the project would have generated USD 5.0m on that day had it been operating, then the rate of accrual for the delay LDs is not effective in compensating for the lost revenues.

Similarly, if the project is completed and handed over to the owner underperforming relative to its guaranteed performance level by 2%, the NPV of free cash flows after opex at the guaranteed performance level is USD 1.0 billion (using the WACC as the discount rate, perhaps), and the rate of accrual of performance LDs is USD 25m / percentage point downside performance, then, per percentage point downside performance, the project will lose USD 20m NPV over its lifetime, but will gain USD 25m immediately, and the rate of accrual of the LDs will therefore be effective in replacing the forfeited revenue stream.

To establish effectiveness, one normally needs to refer to the schedules of the construction, operations or supply contract.

In some instances it is not appropriate to use lost revenue as a comparator –  for example where liquidated damages are payable for failure to deliver under a small supply contract. More on this near the bottom of this article.

Importance:

Is the cap on liability sufficiently high so as to make the guarantees meaningful?

Simply put, if the cap on delay LDs means that the delay LDs run out after one week, then the delay LDs are not meaningful. Similarly, if the performance guarantee cap is low such that only very little downside performance revenue loss is covered by the contractor, then the performance LDs are not meaningful. Determining a level of meaningful guarantees is best done with the assistance of a technical advisor and the project model, which, in conjunction can tell the owner or lender what sort of underperformance is possible or likely, and the impact thereof.

To establish importance, look for the limitation of liability clause of the construction, operations or supply contract.

Reliance:

Finally, assuming the rate of accrual and the cap on guarantees are suitable (or sufficient), we should ask ourselves whether we are able to place reliance on the guarantor or security. If an on-demand bank guarantee has been provided as security for the guarantees, then we can most likely place significant reliance on the guarantees, at least until the amount of the bond has been exceeded. Thereafter, we may need to look to the credit quality of the contractor, or, if a Parent Company Guarantee has been provided, to the credit quality of the parent. There is a significant difference between an on-demand guarantee and a PCG, even from a very creditworthy parent. In the former case, the project (and vicariously, the lenders) may simply deliver the bank guarantee to the guarantor and demand the funds, whereas in the second instance, litigation or at least negotiation may be required.

Other considerations:

Note that a rate of accrual or a cap sufficient to transfer all risk of delay or underperformance to the contractor may not be available. In such instances, it is desirable, if only as second prize, to ensure that the guarantees are sufficiently robust so as to significantly incentivise the contractor to meet his performance guarantees.

Situations like this arise for contracts which have a small value relative to project revenues, but which would prevent the operation of the project if the services provided are absent. If the services under such a contract can be replicated, the guarantees may be sized to cover the difference in price between the original contract and the (possibly temporary) replacement. Example of such a contract may be a water supply contract, or a limestone supply contract for a coal power station.

However, projects may have vital contracts with no available replacement and a small contract value, for which guarantees provide very little risk mitigation, other than alignment of incentives. An example of such a contract is a pipeline/transport agreement for a gas powered power plant. In such instances, incentivisation may be all that is possible.